Informatics Educational Institutions & Programs
Contents
| kilogram | |
|---|---|
 A series of 5, 2, 1, 0.5 and 0.2 kilogram weights, made out of rusty cast iron | |
| General information | |
| Unit system | SI |
| Unit of | mass |
| Symbol | kg |
| Conversions | |
| 1 kg in ... | ... is equal to ... |
| Avoirdupois | ≈ 2.204623 pounds[Note 1] |
| British Gravitational | ≈ 0.0685 slugs |
| CGS units | 1000 grams |
| Atomic mass units | 6.02214076×1026 Da |
The kilogram (also kilogramme[1]) is the base unit of mass in the International System of Units (SI), having the unit symbol kg. It is a widely used measure in science, engineering and commerce worldwide, and is often simply called a kilo colloquially.[2] It means 'one thousand grams'.
The kilogram is defined in terms of the Planck constant, the second, and the metre, both of which are based on fundamental physical constants. This allows a properly equipped metrology laboratory to calibrate a mass measurement instrument such as a Kibble balance as the primary standard to determine an exact kilogram mass.[3][4]
The kilogram was originally defined in 1795 during the French Revolution as the mass of one litre of water. The current definition of a kilogram agrees with this original definition to within 30 parts per million. In 1799, the platinum Kilogramme des Archives replaced it as the standard of mass. In 1889, a cylinder of platinum-iridium, the International Prototype of the Kilogram (IPK), became the standard of the unit of mass for the metric system and remained so for 130 years, before the current standard was adopted in 2019.[5]
Definition
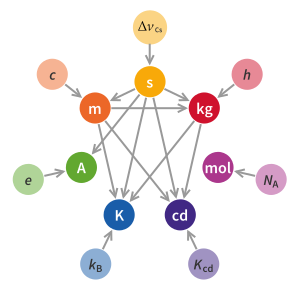
The kilogram is defined in terms of three fundamental physical constants:
- a specific atomic transition frequency ΔνCs, which defines the duration of the second,[6]
- the speed of light c, which when combined with the second, defines the length of the metre,[6]
- and the Planck constant h, which when combined with the metre and second, defines the mass of the kilogram.[6]
The formal definition according to the General Conference on Weights and Measures (CGPM) is:
The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of c and ΔνCs.
Defined in term of those units, the kg is formulated as:[9]
- kg = (299792458)2/(6.62607015×10−34)(9192631770)hΔνCs/c2 = 917097121160018/621541050725904751042hΔνCs/c2 ≈ (1.475521399735270×1040)hΔνCs/c2 .
This definition is generally consistent with previous definitions: the mass remains within 30 ppm of the mass of one litre of water.[10]
Timeline of previous definitions

- 1793: The grave (the precursor of the kilogram) was defined as the mass of 1 litre (dm3) of water, which was determined to be 18841 grains.[11]
- 1795: the gram (1/1000 of a kilogram) was provisionally defined as the mass of one cubic centimetre of water at the melting point of ice.[12]
- 1799: The Kilogramme des Archives was manufactured as a prototype. It had a mass equal to the mass of 1 dm3 of water at the temperature of its maximum density, which is approximately 4 °C.[13]
- 1875–1889: The Metre Convention was signed in 1875, leading to the production of the International Prototype of the Kilogram (IPK) in 1879 and its adoption in 1889.[14]
- 2019: The kilogram was defined in terms of the Planck constant, the speed of light and hyperfine transition frequency of 133Cs as approved by the General Conference on Weights and Measures (CGPM) on November 16, 2018.[5]
Name and terminology
The kilogram is the only base SI unit with an SI prefix (kilo) as part of its name. The word kilogramme or kilogram is derived from the French kilogramme,[15] which itself was a learned coinage, prefixing the Greek stem of χίλιοι khilioi "a thousand" to gramma, a Late Latin term for "a small weight", itself from Greek γράμμα.[16] The word kilogramme was written into French law in 1795, in the Decree of 18 Germinal,[17] which revised the provisional system of units introduced by the French National Convention two years earlier, where the gravet had been defined as weight (poids) of a cubic centimetre of water, equal to 1/1000 of a grave.[18] In the decree of 1795, the term gramme thus replaced gravet, and kilogramme replaced grave.[13]
The French spelling was adopted in Great Britain when the word was used for the first time in English in 1795,[19][15] with the spelling kilogram being adopted in the United States. In the United Kingdom both spellings are used, with "kilogram" having become by far the more common.[1] UK law regulating the units to be used when trading by weight or measure does not prevent the use of either spelling.[20]
In the 19th century the French word kilo, a shortening of kilogramme, was imported into the English language where it has been used to mean both kilogram[21] and kilometre[citation needed].[22] While kilo as an alternative is acceptable, to The Economist for example,[23] the Canadian government's Termium Plus system states that "SI (International System of Units) usage, followed in scientific and technical writing" does not allow its usage and it is described as "a common informal name" on Russ Rowlett's Dictionary of Units of Measurement.[24][25] When the United States Congress gave the metric system legal status in 1866, it permitted the use of the word kilo as an alternative to the word kilogram,[26] but in 1990 revoked the status of the word kilo.[27]
The SI system was introduced in 1960 and in 1970 the BIPM started publishing the SI Brochure, which contains all relevant decisions and recommendations by the CGPM concerning units. The SI Brochure states that "It is not permissible to use abbreviations for unit symbols or unit names ...".[28][Note 2]
Redefinition based on fundamental constants

The replacement of the International Prototype of the Kilogram (IPK) as the primary standard was motivated by evidence accumulated over a long period of time that the mass of the IPK and its replicas had been changing; the IPK had diverged from its replicas by approximately 50 micrograms since their manufacture late in the 19th century. This led to several competing efforts to develop measurement technology precise enough to warrant replacing the kilogram artefact with a definition based directly on physical fundamental constants.[5]
The International Committee for Weights and Measures (CIPM) approved a redefinition of the SI base units in November 2018 that defines the kilogram by defining the Planck constant to be exactly 6.62607015×10−34 kg⋅m2⋅s−1, effectively defining the kilogram in terms of the second and the metre. The new definition took effect on May 20, 2019.[5][7][29]
Prior to the redefinition, the kilogram and several other SI units based on the kilogram were defined by a man-made metal artifact: the Kilogramme des Archives from 1799 to 1889, and the IPK from 1889 to 2019.[5]
In 1960, the metre, previously similarly having been defined with reference to a single platinum-iridium bar with two marks on it, was redefined in terms of an invariant physical constant (the wavelength of a particular emission of light emitted by krypton,[30] and later the speed of light) so that the standard can be independently reproduced in different laboratories by following a written specification.
At the 94th Meeting of the CIPM in 2005, it was recommended that the same be done with the kilogram.[31]
In October 2010, the CIPM voted to submit a resolution for consideration at the General Conference on Weights and Measures (CGPM), to "take note of an intention" that the kilogram be defined in terms of the Planck constant, h (which has dimensions of energy times time, thus mass × length2 / time) together with other physical constants.[32][33] This resolution was accepted by the 24th conference of the CGPM[34] in October 2011 and further discussed at the 25th conference in 2014.[35][36] Although the Committee recognised that significant progress had been made, they concluded that the data did not yet appear sufficiently robust to adopt the revised definition, and that work should continue to enable the adoption at the 26th meeting, scheduled for 2018.[35] Such a definition would theoretically permit any apparatus that was capable of delineating the kilogram in terms of the Planck constant to be used as long as it possessed sufficient precision, accuracy and stability. The Kibble balance is one way to do this.[37]
As part of this project, a variety of very different technologies and approaches were considered and explored over many years. Some of these approaches were based on equipment and procedures that would enable the reproducible production of new, kilogram-mass prototypes on demand (albeit with extraordinary effort) using measurement techniques and material properties that are ultimately based on, or traceable to, physical constants. Others were based on devices that measured either the acceleration or weight of hand-tuned kilogram test masses and which expressed their magnitudes in electrical terms via special components that permit traceability to physical constants. All approaches depend on converting a weight measurement to a mass and therefore require precise measurement of the strength of gravity in laboratories (gravimetry). All approaches would have precisely fixed one or more constants of nature at a defined value.[citation needed]
SI multiples
Because an SI unit may not have multiple prefixes (see SI prefix), prefixes are added to gram, rather than the base unit kilogram, which already has a prefix as part of its name.[38] For instance, one-millionth of a kilogram is 1 mg (one milligram), not 1 μkg (one microkilogram).
| Submultiples | Multiples | ||||
|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name |
| 10−1 g | dg | decigram | 101 g | dag | decagram |
| 10−2 g | cg | centigram | 102 g | hg | hectogram |
| 10−3 g | mg | milligram | 103 g | kg | kilogram |
| 10−6 g | μg | microgram | 106 g | Mg | megagram (tonne) |
| 10−9 g | ng | nanogram | 109 g | Gg | gigagram |
| 10−12 g | pg | picogram | 1012 g | Tg | teragram |
| 10−15 g | fg | femtogram | 1015 g | Pg | petagram |
| 10−18 g | ag | attogram | 1018 g | Eg | exagram |
| 10−21 g | zg | zeptogram | 1021 g | Zg | zettagram |
| 10−24 g | yg | yoctogram | 1024 g | Yg | yottagram |
| 10−27 g | rg | rontogram | 1027 g | Rg | ronnagram |
| 10−30 g | qg | quectogram | 1030 g | Qg | quettagram |
| Common prefixed units are in bold face.[Note 3] | |||||
Practical issues with SI weight names
- Serious medication errors have been made by confusing milligrams and micrograms when micrograms has been abbreviated.[39] The abbreviation "mcg" rather than the SI symbol "μg" is formally mandated for medical practitioners in the US by the Joint Commission on Accreditation of Healthcare Organizations (JCAHO).[40] In the United Kingdom, the National Institute for Health and Care Excellence and Scottish Palliative Care Guidelines state that "micrograms" and "nanograms" must both be written in full, and never abbreviated as "mcg" or "μg".[39][41]
- The hectogram (100 g) (Italian: ettogrammo or etto) is a very commonly used unit in the retail food trade in Italy.[42][43][44]
- The former standard spelling and abbreviation "deka-" and "dk" produced abbreviations such as "dkm" (dekametre) and "dkg" (dekagram).[45] As of 2020, the abbreviation "dkg" (10 g) is still used in parts of central Europe in retail for some foods such as cheese and meat.[46][47][48][49][50]
- The unit name megagram is rarely used, and even then typically only in technical fields in contexts where especially rigorous consistency with the SI standard is desired. For most purposes, the name tonne is instead used. The tonne and its symbol, "t", were adopted by the CIPM in 1879. It is a non-SI unit accepted by the BIPM for use with the SI. According to the BIPM, "This unit is sometimes referred to as 'metric ton' in some English-speaking countries."[51]
See also
- Inertia – Fundamental principle of classical physics
- Kibble balance – Electromechanical weight measuring instrument
- Kilogram-force – Weight on earth of a one-kilogram mass
- Mass versus weight – Distinction between mass and weight
- Metric system – Metre-based systems of measurement
- National Institute of Standards and Technology – Measurement standards laboratory in the United States (NIST)
- Newton – Unit of force in physics
- Standard gravity – Standard gravitational acceleration on Earth
- Weight – Force on a mass due to gravity
Notes
- ^ The avoirdupois pound is part of both United States customary system of units and the Imperial system of units. It is defined as exactly 0.45359237 kilograms.
- ^ The French text (which is the authoritative text) states "Il n'est pas autorisé d'utiliser des abréviations pour les symboles et noms d'unités ..."
- ^ Criterion: A combined total of at least five occurrences on the British National Corpus and the Corpus of Contemporary American English, including both the singular and the plural for both the -gram and the -gramme spelling.
References
- ^ a b "Kilogram". Oxford Dictionaries. Archived from the original on January 31, 2013. Retrieved November 3, 2011.
- ^ Merriam-Mebster definition of Kilo
- ^ "The Latest: Landmark Change to Kilogram Approved". AP News. Associated Press. November 16, 2018. Retrieved March 4, 2020.
- ^ "Mise en pratique for the definition of the kilogram in the SI". BIPM.org. July 7, 2021. Retrieved February 18, 2022.
- ^ a b c d e Resnick, Brian (May 20, 2019). "The new kilogram just debuted. It's a massive achievement". vox.com. Retrieved May 23, 2019.
- ^ a b c International Bureau of Weights and Measures (May 20, 2019), The International System of Units (SI) (PDF) (9th ed.), ISBN 978-92-822-2272-0, archived from the original on October 18, 2021
- ^ a b Draft Resolution A "On the revision of the International System of units (SI)" to be submitted to the CGPM at its 26th meeting (2018) (PDF), archived (PDF) from the original on April 2, 2021
- ^ Decision CIPM/105-13 (October 2016). The day is the 144th anniversary of the Metre Convention.
- ^ SI Brochure: The International System of Units (SI). BIPM, 9th edition, 2019.
- ^ The density of water is 0.999972 g/cm3 at 3.984 °C. See Franks, Felix (2012). The Physics and Physical Chemistry of Water. Springer. ISBN 978-1-4684-8334-5.
- ^ Guyton; Lavoisier; Monge; Berthollet; et al. (1792). Annales de chimie ou Recueil de mémoires concernant la chimie et les arts qui en dépendent. Vol. 15–16. Paris: Chez Joseph de Boffe. p. 277.
- ^ Gramme, le poids absolu d'un volume d'eau pure égal au cube de la centième partie du mètre, et à la température de la glace fondante
- ^ a b Zupko, Ronald Edward (1990). Revolution in Measurement: Western European Weights and Measures Since the Age of Science. Philadelphia: American Philosophical Society. ISBN 978-0-87169-186-6.
- ^ "Treaty of the Metre". Encyclopædia Britannica. 2023. Retrieved July 18, 2023.
- ^ a b "Kilogram". Oxford English Dictionary. Oxford University Press. Retrieved November 3, 2011.
- ^ Fowlers, HW; Fowler, FG (1964). The Concise Oxford Dictionary. Oxford: The Clarendon Press. Greek γράμμα (as it were γράφ-μα, Doric γράθμα) means "something written, a letter", but it came to be used as a unit of weight, apparently equal to 1/24 of an ounce (1/288 of a libra, which would correspond to about 1.14 grams in modern units), at some time during Late Antiquity. French gramme was adopted from Latin gramma, itself quite obscure, but found in the Carmen de ponderibus et mensuris (8.25) attributed by Remmius Palaemon (fl. 1st century), where it is the weight of two oboli (Charlton T. Lewis, Charles Short, A Latin Dictionary s.v. "gramma", 1879). Henry George Liddell. Robert Scott. A Greek-English Lexicon (revised and augmented edition, Oxford, 1940) s.v. γράμμα, citing the 10th-century work Geoponica and a 4th-century papyrus edited in L. Mitteis, Griechische Urkunden der Papyrussammlung zu Leipzig, vol. i (1906), 62 ii 27.
- ^ "Décret relatif aux poids et aux mesures du 18 germinal an 3 (7 avril 1795)" [Decree of 18 Germinal, year III (April 7, 1795) regarding weights and measures]. Grandes lois de la République (in French). Digithèque de matériaux juridiques et politiques, Université de Perpignan. Retrieved November 3, 2011.
- ^ Convention nationale, décret du 1er août 1793, ed. Duvergier, Collection complète des lois, décrets, ordonnances, règlemens avis du Conseil d'état, publiée sur les éditions officielles du Louvre, vol. 6 (2nd ed. 1834), p. 70. The metre (mètre) on which this definition depends was itself defined as the ten-millionth part of a quarter of Earth's meridian, given in traditional units as 3 pieds, 11.44 lignes (a ligne being the 12th part of a pouce (inch), or the 144th part of a pied.
- ^ Peltier, Jean-Gabriel (1795). "Paris, during the year 1795". Monthly Review. 17: 556. Retrieved August 2, 2018. Contemporaneous English translation of the French decree of 1795
- ^ "Spelling of "gram", etc". Weights and Measures Act 1985. Her Majesty's Stationery Office. October 30, 1985. Retrieved November 6, 2011.
- ^ "kilo (n1)". Oxford English Dictionary (2nd ed.). Oxford: Oxford University Press. 1989. Retrieved November 8, 2011.
- ^ "kilo (n2)". Oxford English Dictionary (2nd ed.). Oxford: Oxford University Press. 1989. Retrieved November 8, 2011.
- ^ "Style Guide" (PDF). The Economist. January 7, 2002. Archived from the original (PDF) on July 1, 2017. Retrieved November 8, 2011.
- ^ "kilogram, kg, kilo". Termium Plus. Government of Canada. October 8, 2009. Retrieved May 29, 2019.
- ^ "kilo". How Many?. Archived from the original on November 16, 2011. Retrieved November 6, 2011.
- ^
29th Congress of the United States, Session 1 (May 13, 1866). "H.R. 596, An Act to authorize the use of the metric system of weights and measures". Archived from the original on July 5, 2015.
{{cite web}}: CS1 maint: numeric names: authors list (link) - ^
"Metric System of Measurement:Interpretation of the International System of Units for the United States; Notice" (PDF). Federal Register. 63 (144): 40340. July 28, 1998. Archived from the original (PDF) on October 15, 2011. Retrieved November 10, 2011.
Obsolete Units As stated in the 1990 Federal Register notice, ...
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 130, ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Pallab Ghosh (November 16, 2018). "Kilogram gets a new definition". BBC News. Retrieved November 16, 2018.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 112, ISBN 92-822-2213-6, archived (PDF) from the original on June 4, 2021, retrieved December 16, 2021
- ^ Recommendation 1: Preparative steps towards new definitions of the kilogram, the ampere, the kelvin and the mole in terms of fundamental constants (PDF). 94th meeting of the International Committee for Weights and Measures. October 2005. p. 233. Archived (PDF) from the original on June 30, 2007. Retrieved February 7, 2018.
- ^ "NIST Backs Proposal for a Revamped System of Measurement Units". NIST. Nist.gov. October 26, 2010. Retrieved April 3, 2011.
- ^ Ian Mills (September 29, 2010). "Draft Chapter 2 for SI Brochure, following redefinitions of the base units" (PDF). CCU. Retrieved January 1, 2011.
- ^ Resolution 1 – On the possible future revision of the International System of Units, the SI (PDF). 24th meeting of the General Conference on Weights and Measures. Sèvres, France. October 17–21, 2011. Retrieved October 25, 2011.
- ^ a b "BIPM – Resolution 1 of the 25th CGPM". www.bipm.org. Retrieved March 27, 2017.
- ^ "General Conference on Weights and Measures approves possible changes to the International System of Units, including redefinition of the kilogram" (PDF) (Press release). Sèvres, France: General Conference on Weights and Measures. October 23, 2011. Retrieved October 25, 2011.
- ^ Robinson, Ian A.; Schlamminger, Stephan (2016). "The watt or Kibble balance: A technique for implementing the new SI definition of the unit of mass". Metrologia. 53 (5): A46–A74. Bibcode:2016Metro..53A..46R. doi:10.1088/0026-1394/53/5/A46. PMC 8752041. PMID 35023879.
- ^ BIPM: SI Brochure: Section 3.2, The kilogram Archived March 29, 2016, at the Wayback Machine
- ^ a b "Prescribing Information for Liquid Medicines". Scottish Palliative Care Guidelines. Archived from the original on July 10, 2018. Retrieved June 15, 2015.
- ^ "New Joint Commission "Do Not Use" List: Abbreviations, Acronyms, and Symbols". American Academy of Physical Medicine and Rehabilitation. Archived from the original on September 15, 2015. Retrieved February 19, 2024.
- ^ "Prescription writing". National Institute for Health and Care Excellence. Retrieved February 19, 2024.
- ^ Tom Stobart, The Cook's Encyclopedia, 1981, p. 525
- ^ J.J. Kinder, V.M. Savini, Using Italian: A Guide to Contemporary Usage, 2004, ISBN 0521485568, p. 231
- ^ Giacomo Devoto, Gian Carlo Oli, Nuovo vocabolario illustrato della lingua italiana, 1987, s.v. 'ètto': "frequentissima nell'uso comune: un e. di caffè, un e. di mortadella; formaggio a 2000 lire l'etto"
- ^ U.S. National Bureau of Standards, The International Metric System of Weights and Measures, "Official Abbreviations of International Metric Units", 1932, p. 13
- ^ "Jestřebická hovězí šunka 10 dkg | Rancherské speciality". eshop.rancherskespeciality.cz (in Czech). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ "Sedliacka šunka 1 dkg | Gazdovský dvor – Farma Busov Gaboltov". Sedliacka šunka 1 dkg (in Slovak). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ "sýr bazalkový – Farmářské Trhy". www.e-farmarsketrhy.cz (in Czech). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ "Termékek – Csíz Sajtműhely" (in Hungarian). Archived from the original on June 16, 2020. Retrieved June 16, 2020.
- ^ Non-SI units that are accepted for use with the SI, SI Brochure: Section 4 (Table 8), BIPM
External links
- NIST Improves Accuracy of 'Watt Balance' Method for Defining the Kilogram
- The UK's National Physical Laboratory (NPL): Are any problems caused by having the kilogram defined in terms of a physical artefact? (FAQ – Mass & Density)
- NPL: NPL Kibble balance
- Metrology in France: Watt balance
- Australian National Measurement Institute: Redefining the kilogram through the Avogadro constant
- International Bureau of Weights and Measures (BIPM): Home page
- NZZ Folio: What a kilogram really weighs
- NPL: What are the differences between mass, weight, force and load?
- BBC: Getting the measure of a kilogram
- NPR: This Kilogram Has A Weight-Loss Problem, an interview with National Institute of Standards and Technology physicist Richard Steiner
- Avogadro and molar Planck constants for the redefinition of the kilogram
- Realization of the awaited definition of the kilogram
- Sample, Ian (November 9, 2018). "In the balance: scientists vote on first change to kilogram in a century". The Guardian. Retrieved November 9, 2018.
Videos
- The BIPM – YouTube channel
- "The role of the Planck constant in physics" – presentation at 26th CGPM meeting at Versailles, France, November 2018 when voting on superseding the IPK took place on YouTube