Informatics Educational Institutions & Programs
Contents
The Lotka–Volterra equations, also known as the Lotka–Volterra predator–prey model, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
where
- the variable x is the population density of prey (for example, the number of rabbits per square kilometre);
- the variable y is the population density of some predator (for example, the number of foxes per square kilometre);
- and represent the instantaneous growth rates of the two populations;
- t represents time;
- The prey's parameters, α and β, describe, respectively, the maximum prey per capita growth rate, and the effect of the presence of predators on the prey death rate.
- The predator's parameters, γ, δ, respectively describe the predator's per capita death rate, and the effect of the presence of prey on the predator's growth rate.
- All parameters are positive and real.
The solution of the differential equations is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.[1]
The Lotka–Volterra system of equations is an example of a Kolmogorov model,[2][3][4] which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism.
Biological interpretation and model assumptions
The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation on the prey is assumed to be proportional to the rate at which the predators and the prey meet; this is represented above by βxy. If either x or y is zero, then there can be no predation. With these two terms the prey equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the rate at which it is preyed upon.
The term δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used, as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). The term γy represents the loss rate of the predators due to either natural death or emigration; it leads to an exponential decay in the absence of prey. Hence the equation expresses that the rate of change of the predator's population depends upon the rate at which it consumes prey, minus its intrinsic death rate.
The Lotka–Volterra predator-prey model makes a number of assumptions about the environment and biology of the predator and prey populations:[5]
- The prey population finds ample food at all times.
- The food supply of the predator population depends entirely on the size of the prey population.
- The rate of change of population is proportional to its size.
- During the process, the environment does not change in favour of one species, and genetic adaptation is inconsequential.
- Predators have limitless appetite.
- Both populations can be described by a single variable. This amounts to assuming that the populations do not have a spatial or age distribution that contributes to the dynamics.
Biological relevance of the model
None of the assumptions above are likely to hold for natural populations. Nevertheless, the Lotka–Volterra model shows two important properties of predator and prey populations and these properties often extend to variants of the model in which these assumptions are relaxed:
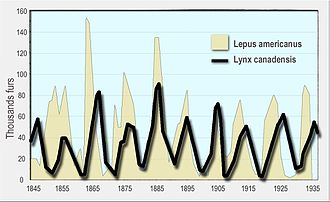
Firstly, the dynamics of predator and prey populations have a tendency to oscillate. Fluctuating numbers of predators and prey have been observed in natural populations, such as the lynx and snowshoe hare data of the Hudson's Bay Company[6] and the moose and wolf populations in Isle Royale National Park.[7]
Secondly, the population equilibrium of this model has the property that the prey equilibrium density (given by ) depends on the predator's parameters, and the predator equilibrium density (given by ) on the prey's parameters. This has as a consequence that an increase in, for instance, the prey growth rate, , leads to an increase in the predator equilibrium density, but not the prey equilibrium density. Making the environment better for the prey benefits the predator, not the prey (this is related to the paradox of the pesticides and to the paradox of enrichment). A demonstration of this phenomenon is provided by the increased percentage of predatory fish caught had increased during the years of World War I (1914–18), when prey growth rate was increased due to a reduced fishing effort.
A further example is provided by the experimental iron fertilization of the ocean. In several experiments large amounts of iron salts were dissolved in the ocean. The expectation was that iron, which is a limiting nutrient for phytoplankton, would boost growth of phytoplankton and that it would sequester carbon dioxide from the atmosphere. The addition of iron typically leads to a short bloom in phyoplankton, which is quickly consumed by other organisms (such as small fish or zooplankton) and limits the effect of enrichment mainly to increased predator density, which in turn limits the carbon sequestration. This is as predicted by the equilibrium population densities of the Lotka–Volterra predator-prey model, and is a feature that carries over to more elaborate models in which the restrictive assumptions of the simple model are relaxed.[8]
Applications to economics and marketing
The Lotka–Volterra model has additional applications to areas such as economics[9] and marketing.[10][11] It can be used to describe the dynamics in a market with several competitors, complementary platforms and products, a sharing economy, and more. There are situations in which one of the competitors drives the other competitors out of the market and other situations in which the market reaches an equilibrium where each firm stabilizes on its market share. It is also possible to describe situations in which there are cyclical changes in the industry or chaotic situations with no equilibrium and changes are frequent and unpredictable.
History
The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka in the theory of autocatalytic chemical reactions in 1910.[12][13] This was effectively the logistic equation,[14] originally derived by Pierre François Verhulst.[15] In 1920 Lotka extended the model, via Andrey Kolmogorov, to "organic systems" using a plant species and a herbivorous animal species as an example[16] and in 1925 he used the equations to analyse predator–prey interactions in his book on biomathematics.[17] The same set of equations was published in 1926 by Vito Volterra, a mathematician and physicist, who had become interested in mathematical biology.[13][18][19] Volterra's enquiry was inspired through his interactions with the marine biologist Umberto D'Ancona, who was courting his daughter at the time and later was to become his son-in-law. D'Ancona studied the fish catches in the Adriatic Sea and had noticed that the percentage of predatory fish caught had increased during the years of World War I (1914–18). This puzzled him, as the fishing effort had been very much reduced during the war years and, as prey fish the preferred catch, one would intuitively expect this to increase of prey fish percentage. Volterra developed his model to explain D'Ancona's observation and did this independently from Alfred Lotka. He did credit Lotka's earlier work in his publication, after which the model has become known as the "Lotka-Volterra model".[20]
The model was later extended to include density-dependent prey growth and a functional response of the form developed by C. S. Holling; a model that has become known as the Rosenzweig–MacArthur model.[21] Both the Lotka–Volterra and Rosenzweig–MacArthur models have been used to explain the dynamics of natural populations of predators and prey.
In the late 1980s, an alternative to the Lotka–Volterra predator–prey model (and its common-prey-dependent generalizations) emerged, the ratio dependent or Arditi–Ginzburg model.[22] The validity of prey- or ratio-dependent models has been much debated.[23]
The Lotka–Volterra equations have a long history of use in economic theory; their initial application is commonly credited to Richard Goodwin in 1965[24] or 1967.[25][26]
Solutions to the equations
The equations have periodic solutions. These solutions do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.[27][28][29]
If none of the non-negative parameters α, β, γ, δ vanishes, three can be absorbed into the normalization of variables to leave only one parameter: since the first equation is homogeneous in x, and the second one in y, the parameters β/α and δ/γ are absorbable in the normalizations of y and x respectively, and γ into the normalization of t, so that only α/γ remains arbitrary. It is the only parameter affecting the nature of the solutions.
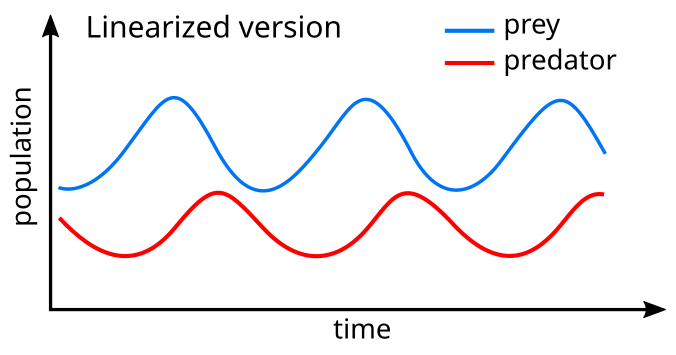
A linearization of the equations yields a solution similar to simple harmonic motion[30] with the population of predators trailing that of prey by 90° in the cycle.
A simple example


Suppose there are two species of animals, a rabbit (prey) and a fox (predator). If the initial densities are 10 rabbits and 10 foxes per square kilometre, one can plot the progression of the two species over time; given the parameters that the growth and death rates of rabbits are 1.1 and 0.4 while that of foxes are 0.1 and 0.4 respectively. The choice of time interval is arbitrary.
One may also plot solutions parametrically as orbits in phase space, without representing time, but with one axis representing the number of prey and the other axis representing the densities of predators for all times.
This corresponds to eliminating time from the two differential equations above to produce a single differential equation
relating the variables x and y. The solutions of this equation are closed curves. It is amenable to separation of variables: integrating
yields the implicit relationship
where V is a constant quantity depending on the initial conditions and conserved on each curve.
An aside: These graphs illustrate a serious potential limitation in the application as a biological model: for this specific choice of parameters, in each cycle, the rabbit population is reduced to extremely low numbers, yet recovers (while the fox population remains sizeable at the lowest rabbit density). In real-life situations, however, chance fluctuations of the discrete numbers of individuals might cause the rabbits to actually go extinct, and, by consequence, the foxes as well. This modelling problem has been called the "atto-fox problem", an atto-fox being a notional 10−18 of a fox.[31][32] A density of 10−18 foxes per square kilometre equates to an average of approximately 5×10−10 foxes on the surface of the earth, which in practical terms means that foxes are extinct.
Hamiltonian structure of the system
Since the quantity is conserved over time, it plays role of a Hamiltonian function of the system.[33] To see this we can define Poisson bracket as follows . Then Hamilton's equations read
Phase-space plot of a further example

A less extreme example covers:
α = 2/3, β = 4/3, γ = 1 = δ. Assume x, y quantify thousands each. Circles represent prey and predator initial conditions from x = y = 0.9 to 1.8, in steps of 0.1. The fixed point is at (1, 1/2).
Dynamics of the system
In the model system, the predators thrive when prey is plentiful but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a population cycle of growth and decline.
Population equilibrium
Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0:
The above system of equations yields two solutions:
Hence, there are two equilibria.
The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.
Stability of the fixed points
The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives.
The Jacobian matrix of the predator–prey model is
First fixed point (extinction)
When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes
The eigenvalues of this matrix are
In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.
The instability of this fixed point is of significance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, it follows that the extinction of both species is difficult in the model. (In fact, this could only occur if the prey were artificially completely eradicated, causing the predators to die of starvation. If the predators were eradicated, the prey population would grow without bound in this simple model.) The populations of prey and predator can get infinitesimally close to zero and still recover.
Second fixed point (oscillations)
Evaluating J at the second fixed point leads to
The eigenvalues of this matrix are
As the eigenvalues are both purely imaginary and conjugate to each other, this fixed point must either be a center for closed orbits in the local vicinity or an attractive or repulsive spiral. In conservative systems, there must be closed orbits in the local vicinity of fixed points that exist at the minima and maxima of the conserved quantity. The conserved quantity is derived above to be on orbits. Thus orbits about the fixed point are closed and elliptic, so the solutions are periodic, oscillating on a small ellipse around the fixed point, with a frequency and period .
As illustrated in the circulating oscillations in the figure above, the level curves are closed orbits surrounding the fixed point: the levels of the predator and prey populations cycle and oscillate without damping around the fixed point with frequency .
The value of the constant of motion V, or, equivalently, K = exp(−V), , can be found for the closed orbits near the fixed point.
Increasing K moves a closed orbit closer to the fixed point. The largest value of the constant K is obtained by solving the optimization problem
See also
- Competitive Lotka–Volterra equations
- Generalized Lotka–Volterra equation
- Mutualism and the Lotka–Volterra equation
- Community matrix
- Population dynamics
- Population dynamics of fisheries
- Nicholson–Bailey model
- Reaction–diffusion system
- Paradox of enrichment
- Lanchester's laws, a similar system of differential equations for military forces
- Random generalized Lotka–Volterra model
- Consumer-resource model
Notes
- ^ Cooke, D.; Hiorns, R. W.; et al. (1981). The Mathematical Theory of the Dynamics of Biological Populations. Vol. II. Academic Press.
- ^ Freedman, H. I. (1980). Deterministic Mathematical Models in Population Ecology. Marcel Dekker.
- ^ Brauer, F.; Castillo-Chavez, C. (2000). Mathematical Models in Population Biology and Epidemiology. Springer-Verlag.
- ^ Hoppensteadt, F. (2006). "Predator-prey model". Scholarpedia. 1 (10): 1563. Bibcode:2006SchpJ...1.1563H. doi:10.4249/scholarpedia.1563.
- ^ "PREDATOR-PREY DYNAMICS". www.tiem.utk.edu. Retrieved 2018-01-09.
- ^ Gilpin, M. E. (1973). "Do hares eat lynx?". American Naturalist. 107 (957): 727–730. doi:10.1086/282870. S2CID 84794121.
- ^ Jost, C.; Devulder, G.; Vucetich, J.A.; Peterson, R.; Arditi, R. (2005). "The wolves of Isle Royale display scale-invariant satiation and density dependent predation on moose". J. Anim. Ecol. 74 (5): 809–816. doi:10.1111/j.1365-2656.2005.00977.x.
- ^ Pan, A.; Pourziaei, B.; Huang, H. (2015-06-03). "Effect of Ocean Iron Fertilization on the Phytoplankton Biological Carbon Pump". Advances in Applied Mathematics and Mechanics. 3 (1): 52–64. doi:10.4208/aamm.10-m1023. S2CID 124606355.
- ^ Prasolov, Alexander V. (2016). Some quantitative methods and models in economic theory. Economic issues, problems and perspectives. New York: Nova Publishers. ISBN 978-1-63484-937-1.
- ^ Hung, Hui-Chih; Chiu, Yu-Chih; Wu, Muh-Cherng (2017). "A Modified Lotka–Volterra Model for Diffusion and Substitution of Multigeneration DRAM Processing Technologies". Mathematical Problems in Engineering. 2017: 1–12. doi:10.1155/2017/3038203. ISSN 1024-123X.
- ^ Orbach, Yair (2022). Forecasting the Dynamics of Market and Technology. Israel: Ariel University Press. pp. 123–143. ISBN 978-965-7632-40-6.
- ^ Lotka, A. J. (1910). "Contribution to the Theory of Periodic Reaction". J. Phys. Chem. 14 (3): 271–274. doi:10.1021/j150111a004.
- ^ a b Goel, N. S.; et al. (1971). On the Volterra and Other Nonlinear Models of Interacting Populations. Academic Press. ISBN 0-12-287450-1.
- ^ Berryman, A. A. (1992). "The Origins and Evolution of Predator-Prey Theory" (PDF). Ecology. 73 (5): 1530–1535. doi:10.2307/1940005. JSTOR 1940005. Archived from the original (PDF) on 2010-05-31.
- ^ Verhulst, P. H. (1838). "Notice sur la loi que la population poursuit dans son accroissement". Corresp. Mathématique et Physique. 10: 113–121.
- ^ Lotka, A. J. (1920). "Analytical Note on Certain Rhythmic Relations in Organic Systems". Proc. Natl. Acad. Sci. U.S.A. 6 (7): 410–415. Bibcode:1920PNAS....6..410L. doi:10.1073/pnas.6.7.410. PMC 1084562. PMID 16576509.
- ^ Lotka, A. J. (1925). Elements of Physical Biology. Williams and Wilkins.
- ^ Volterra, V. (1926). "Variazioni e fluttuazioni del numero d'individui in specie animali conviventi". Mem. Acad. Lincei Roma. 2: 31–113.
- ^ Volterra, V. (1931). "Variations and fluctuations of the number of individuals in animal species living together". In Chapman, R. N. (ed.). Animal Ecology. McGraw–Hill.
- ^ Kingsland, S. (1995). Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press. ISBN 978-0-226-43728-6.
- ^ Rosenzweig, M. L.; MacArthur, R.H. (1963). "Graphical representation and stability conditions of predator-prey interactions". American Naturalist. 97 (895): 209–223. doi:10.1086/282272. S2CID 84883526.
- ^ Arditi, R.; Ginzburg, L. R. (1989). "Coupling in predator-prey dynamics: ratio dependence" (PDF). Journal of Theoretical Biology. 139 (3): 311–326. Bibcode:1989JThBi.139..311A. doi:10.1016/s0022-5193(89)80211-5.
- ^ Abrams, P. A.; Ginzburg, L. R. (2000). "The nature of predation: prey dependent, ratio dependent or neither?". Trends in Ecology & Evolution. 15 (8): 337–341. doi:10.1016/s0169-5347(00)01908-x. PMID 10884706.
- ^ Gandolfo, G. (2008). "Giuseppe Palomba and the Lotka–Volterra equations". Rendiconti Lincei. 19 (4): 347–357. doi:10.1007/s12210-008-0023-7. S2CID 140537163.
- ^ Goodwin, R. M. (1967). "A Growth Cycle". In Feinstein, C. H. (ed.). Socialism, Capitalism and Economic Growth. Cambridge University Press.
- ^ Desai, M.; Ormerod, P. (1998). "Richard Goodwin: A Short Appreciation" (PDF). The Economic Journal. 108 (450): 1431–1435. CiteSeerX 10.1.1.423.1705. doi:10.1111/1468-0297.00350. Archived from the original (PDF) on 2011-09-27. Retrieved 2010-03-22.
- ^ Steiner, Antonio; Gander, Martin Jakob (1999). "Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich". Il Volterriano. 7: 32–44.
- ^ Evans, C. M.; Findley, G. L. (1999). "A new transformation for the Lotka-Volterra problem". Journal of Mathematical Chemistry. 25: 105–110. doi:10.1023/A:1019172114300. S2CID 36980176.
- ^ Leconte, M.; Masson, P.; Qi, L. (2022). "Limit cycle oscillations, response time, and the time-dependent solution to the Lotka-Volterra predator-prey model". Physics of Plasmas. 29 (2): 022302. arXiv:2110.11557. doi:10.1063/5.0076085. S2CID 239616189.
- ^ Tong, H. (1983). Threshold Models in Non-linear Time Series Analysis. Springer–Verlag.
- ^ Lobry, Claude; Sari, Tewfik (2015). "Migrations in the Rosenzweig-MacArthur model and the "atto-fox" problem" (PDF). Arima. 20: 95–125.
- ^ Mollison, D. (1991). "Dependence of epidemic and population velocities on basic parameters" (PDF). Math. Biosci. 107 (2): 255–287. doi:10.1016/0025-5564(91)90009-8. PMID 1806118.
- ^ Nutku, I. (1990). "Hamiltonian structure of the Lotka-Volterra equations". Physics Letters A. 145 (1): 27–28. Bibcode:1990PhLA..145...27N. doi:10.1016/0375-9601(90)90270-X. hdl:11693/26204. S2CID 121710034.
- ^ Baigent, Steve (2010-03-02). "Lotka-Volterra Dynamics - An introduction" (PDF).
Further reading
- Hofbauer, Josef; Sigmund, Karl (1998). "Dynamical Systems and Lotka–Volterra Equations". Evolutionary Games and Population Dynamics. New York: Cambridge University Press. pp. 1–54. ISBN 0-521-62570-X.
- Kaplan, Daniel; Glass, Leon (1995). Understanding Nonlinear Dynamics. New York: Springer. ISBN 978-0-387-94440-1.
- Leigh, E. R. (1968). "The ecological role of Volterra's equations". Some Mathematical Problems in Biology. – a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
- Murray, J. D. (2003). Mathematical Biology I: An Introduction. New York: Springer. ISBN 978-0-387-95223-9.'
- Stefano Allesina's Community Ecology course lecture notes: https://stefanoallesina.github.io/Theoretical_Community_Ecology/





















































