Informatics Educational Institutions & Programs
Contents
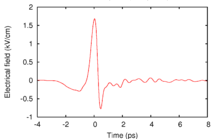
In physics, terahertz time-domain spectroscopy (THz-TDS) is a spectroscopic technique in which the properties of matter are probed with short pulses of terahertz radiation. The generation and detection scheme is sensitive to the sample's effect on both the amplitude and the phase of the terahertz radiation.

Explanation
Typically, an ultrashort pulsed laser is used in the terahertz pulse generation process. In the use of low-temperature grown GaAs as an antenna, the ultrashort pulse creates charge carriers that are accelerated to create the terahertz pulse. In the use of non-linear crystals as a source, a high-intensity ultrashort pulse produces THz radiation from the crystal. A single terahertz pulse can contain frequency components covering much of the terahertz range, often from 0.05 to 4 THz, though the use of an air plasma can yield frequency components up to 40 THz.[1] After THz pulse generation, the pulse is directed by optical techniques, focused through a sample, then measured.
THz-TDS requires generation of an ultrafast (thus, large bandwidth) terahertz pulse from an even faster femtosecond optical pulse, typically from a Ti-sapphire laser. That optical pulse is first split to provide a probe pulse whose path length is adjusted using an optical delay line. The probe pulse strobes the detector that is sensitive to the electric field of the resulting terahertz signal at the time of the optical probe pulse sent to it. By varying the path length traversed by the probe pulse, the test signal is thereby measured as a function of time—the same principle as a sampling oscilloscope (technically, the measurement obtains the convolution of the test signal and the time-domain response of the strobed detector). To obtain the resulting frequency domain response using the Fourier transform, the measurement must cover each point in time (delay-line offset) of the resulting test pulse. The response of a test sample can be calibrated by dividing its spectrum so obtained by the spectrum of the terahertz pulse obtained with the sample removed, for instance.
Components
Components of a typical THz-TDS instrument, as illustrated in the figure, include an infrared laser, optical beamsplitters, beam steering mirrors, delay stages, a terahertz generator, terahertz beam focusing and collimating optics like parabolic mirrors, and detector.

Ti:sapphire laser
Constructing a THz-TDS experiment using low temperature grown GaAs (LT-GaAs) based antennas requires a laser whose photon energy exceeds the band gap of the material. Ti:sapphire lasers tuned to around 800 nm, matching the energy gap in LT-GaAs, are ideal as they can generate optical pulses as short as 10 fs. These lasers are available as commercial, turnkey systems.
Steering mirrors
Silver-coated mirrors are optimum for use as steering mirrors for infrared pulses around 800 nm. Their reflectivity is higher than gold and much higher than aluminum at that wavelength.
Beamsplitters
A beamsplitter is used to divide a single ultrashort optical pulse into two separate beams. A 50/50 beamsplitter is often used, supplying equal optical power to the terahertz generator and detector, though it is common to provide the terahertz generation path with more power given the inefficiency of the terahertz generation process compared to the detection efficiency of infrared (typically 800 nm wavelength) light.
Delay stage
An optical delay-line is implemented using a movable stage to vary the path length of one of the two beam paths. A delay stage uses a moving retroreflector to redirect the beam along a well-defined output path but following a delay. Movement of the stage holding the retroreflector corresponds to an adjustment of path length and consequently the time at which the terahertz detector is gated relative to the source terahertz pulse.
Purge box
A purge box is typically used so that absorption of THz radiation by gaseous water molecules is minimized. A dry air source is often used for this purpose, however, a nitrogen gas source may also be used.
Water is known to have many discrete absorptions in the THz region that are rotational modes of water molecules. Alternatively, nitrogen, as a diatomic molecule, has no electric dipole moment, and does not (for the purposes of typical THz-TDS) absorb THz radiation. Thus, a purge box may be filled with nitrogen gas so no unintended discrete absorptions in the THz frequency range occur.
Parabolic mirrors

Off-axis parabolic mirrors are commonly used to collimate and focus THz radiation. Radiation from an effective point source, such as from a low-temperature gallium arsenide (LT-GaAs) antenna (active region ~5 μm) incident on an off-axis parabolic mirror becomes collimated, while collimated radiation incident on a parabolic mirror is focused to a point (see diagram). Terahertz radiation can thus be manipulated spatially using optical components such as metal-coated mirrors as well as lenses made from materials that are transparent at THz wavelengths. Samples for spectroscopy are commonly placed at a focus where the terahertz beam is most concentrated.
Uses of THz radiation
THz radiation has several distinct advantages for use in spectroscopy. Many materials are transparent at terahertz wavelengths, and this radiation is safe for biological tissue being non-ionizing (as opposed to X-rays). Many interesting materials have unique spectral fingerprints in the terahertz range that may be used for identification. Demonstrated examples include several different types of explosives, dynamic fingerprinting of DNA and protein molecules using polarization varying anisotropic terahertz microspectroscopy,[2] polymorphic forms of many compounds used as active pharmaceutical ingredients (API) in commercial medications as well as several illegal narcotic substances.[3]
Since many materials are transparent to THz radiation, underlying materials can be accessed through visually opaque intervening layers.
Though not strictly a spectroscopic technique, the ultrashort width of THz radiation pulses allows for measurements (e.g., thickness, density, defect location) on difficult-to-probe materials like foam. These measurement capabilities share many similarities to those of pulsed ultrasonic systems as the depth of buried structures can be inferred through timing of their reflections of these short terahertz pulses.
THz generation
There are three widely used techniques for generating terahertz pulses, all based on ultrashort pulses from titanium-sapphire lasers or mode-locked fiber lasers.
Surface emitters
When an ultra-short (100 femtoseconds or shorter) optical pulse illuminates a semiconductor and its wavelength (energy) is above the energy band-gap of the material, it photogenerates mobile carriers. Most carriers are generated near the surface of the material (typically within 1 micrometre) because pulses are absorbed exponentially with respect to depth. This has two main effects. Firstly, it generates a band bending that has the effect of accelerating carriers of different signs in opposite directions (normal to the surface), creating a dipole. This effect is known as surface field emission. Secondly, the presence of a surface creates a break of symmetry that causes carriers to move (on average) only into the bulk of the semiconductor. This phenomenon, combined with the difference of mobilities of electrons and holes, also produces a dipole. This is known as the photo-Dember effect and is particularly strong in high-mobility semiconductors such as indium arsenide.
Photoconductive emitters
When generating THz radiation via a photoconductive emitter, an ultrafast pulse (typically 100 femtoseconds or shorter) creates charge carriers (electron-hole pairs) in a semiconductor material. This incident laser pulse abruptly changes the antenna from an insulating state into a conducting state. Due to an electric bias applied across the antenna, a sudden electric current transmits across the antenna. This changing current lasts for about a picosecond, and thus emits terahertz radiation since the Fourier transform of a picosecond length signal will contain THz components.
Typically the two antenna electrodes are patterned on a low temperature gallium arsenide (LT-GaAs), semi-insulating gallium arsenide (SI-GaAs), or other semiconductor (such as InP) substrate. In a commonly used scheme, the electrodes are formed into the shape of a simple dipole antenna with a gap of a few micrometers and have a bias voltage up to 40 V between them. The ultrafast laser pulse must have a wavelength that is short enough to excite electrons across the bandgap of the semiconductor substrate. This scheme is suitable for illumination with a Ti:sapphire oscillator laser with photon energies of 1.55 eV and pulse energies of about 10 nJ. For use with amplified Ti:sapphire lasers with pulse energies of about 1 mJ, the electrode gap can be increased to several centimeters with a bias voltage of up to 200 kV.
More recent advances towards cost-efficient and compact THz-TDS systems are based on mode-locked fiber laser sources emitting at a center wavelength of 1550 nm. Therefore, the photoconductive emitters must be based on semiconductor materials with smaller band gaps of approximately 0.74 eV such as Fe-doped indium gallium arsenide[4] or indium gallium arsenide/indium aluminum arsenide heterostructures.[5]
The short duration of THz pulses generated (typically ~2 ps) are primarily due to the rapid rise of the photo-induced current in the semiconductor and short carrier lifetime semiconductor materials (e.g., LT-GaAs). This current may persist for only a few hundred femtoseconds to several nanoseconds depending on the substrate material. This is not the only means of generation but is currently (as of 2008) the most common.[citation needed]
Pulses produced by this method have average power levels on the order of several tens of microwatts.[5] The peak power during pulses can be many orders of magnitude higher due to the low duty cycle of mostly >1%, which is dependent on the repetition rate of the laser source. The maximum bandwidth of the resulting THz pulse is primarily limited by the duration of the laser pulse, while the frequency position of the maximum of the Fourier spectrum is determined by the carrier lifetime of the semiconductor.[6]
Optical rectification
In optical rectification, a high-intensity ultrashort laser pulse passes through a transparent crystal material that emits a terahertz pulse without any applied voltages. It is a nonlinear-optical process, where an appropriate crystal material is quickly electrically polarized at high optical intensities. This changing electrical polarization emits terahertz radiation.
Because of the high laser intensities that are necessary, this technique is mostly used with amplified Ti:sapphire lasers. Typical crystal materials are zinc telluride, gallium phosphide, and gallium selenide.
The bandwidth of pulses generated by optical rectification is limited by the laser pulse duration, terahertz absorption in the crystal material, the thickness of the crystal, and a mismatch between the propagation speed of the laser pulse and the terahertz pulse inside the crystal. Typically, a thicker crystal will generate higher intensities, but lower THz frequencies. With this technique, it is possible to boost the generated frequencies to 40 THz (7.5 µm) or higher, although 2 THz (150 µm) is more commonly used since it requires less complex optical setups.
THz detection
The electrical field of terahertz pulses is measured in a detector simultaneously illuminated with an ultrashort laser pulse. Two common detection schemes are used in THz-TDS: photoconductive sampling and electro-optical sampling. The power of THz pulses can be detected by bolometers (heat detectors cooled to liquid-helium temperatures), but since bolometers can only measure the total energy of a terahertz pulse rather than its electric field over time, they are unsuitable for THz-TDS.
Because the measurement technique is coherent, it naturally rejects incoherent radiation. Additionally, because the time slice of the measurement is extremely narrow, the noise contribution to the measurement is extremely low.
The signal-to-noise ratio (S/N) of the resulting time-domain waveform depends on experimental conditions (e.g., averaging time). However due to the coherent sampling techniques described, high S/N values (>70 dB) are routinely observed with 1 minute averaging times.
Downmixing
The original problem responsible for the "Terahertz gap" (the colloquial term for the lack of techniques in the THz frequency range) was that electronics routinely have limited operation at frequencies at and above 1012 Hz. Two experimental parameters make such measurement possible in THz-TDS with LT-GaAs antennas: the femtosecond “gating” pulses and the < 1 ps lifetimes of the charge carriers in the antenna (effectively determining the antenna's “on” time). When all optical path lengths have fixed length, an effective dc current results at the detection electronics due to their low time resolution. Picosecond time resolution does not come from fast electronic or optical techniques, but from the ability to adjust optical path lengths on the micrometer (μm) scale. To measure a particular segment of a THz pulse, the optical path lengths are fixed and the (effective dc) current at the detector due to the a particular segment of electric field of the THz pulse.
THz-TDS measurements are typically not single-shot measurements.
Photoconductive detection
Photoconductive detection is similar to photoconductive generation. Here, the voltage bias across the antenna leads is generated by the electric field of the THz pulse focused onto the antenna, rather than some external generation. The THz electric field drives current across the antenna leads, which is usually amplified with a low-bandwidth amplifier. This amplified current is the measured parameter that corresponds to the THz field strength. Again, the carriers in the semiconductor substrate have an extremely short lifetime. Thus, the THz electric field strength is only sampled for an extremely narrow slice (femtoseconds) of the entire electric field waveform.
Electro-optical sampling
The materials used for generation of terahertz radiation by optical rectification can also be used for its detection by using the Pockels effect, where particular crystalline materials become birefringent in the presence of an electric field. The birefringence caused by the electric field of a terahertz pulse leads to a change in the optical polarization of the detection pulse, proportional to the terahertz electric-field strength. With the help of polarizers and photodiodes, this polarization change is measured.
As with the generation, the bandwidth of the detection is dependent on the laser pulse duration, material properties, and crystal thickness.
Advantages
THz-TDS measures the electric field of a pulse and not just the power. Thus, THz-TDS measures both the amplitude and phase information of the frequency components it contains. In contrast, measuring only the power at each frequency is essentially a photon counting technique; information regarding the phase of the light is not obtained. Thus, the waveform is not uniquely determined by such a power measurement.
Even when measuring only the power reflected from a sample, the complex optical response constant of the material can be obtained. This is so because the complex nature of an optical constant is not arbitrary. The real and imaginary parts of an optical constant are related by the Kramers–Kronig relations. There is a difficulty in applying the Kramers-Kronig relations as written, because information about the sample (reflected power, for example) must be obtained at all frequencies. In practice, far separated frequency regions do not have significant influence on each other, and reasonable limiting conditions can be applied at high and low frequency, outside of the measured range.
THz-TDS, in contrast, does not require use of Kramers-Kronig relations. By measuring the electric field of a THz pulse in the time-domain, the amplitude and phase of each frequency component of the THz pulse are known (in contrast to the single piece of information known by a power measurement). Thus the real and imaginary parts of an optical constant can be known at every frequency within the usable bandwidth of a THz pulse, without need of frequencies outside the usable bandwidth or Kramers-Kronig relations.
See also
References
- ^ Fan, Zhengquan; Lu, Chenhui; Liu, Yi (2022-02-15). "Tunable broadband THz emission from air plasma pumped by femtosecond pulses composed of a fundamental frequency with its detuned second harmonic". Optics Communications. 505: 127532. doi:10.1016/j.optcom.2021.127532. ISSN 0030-4018.
- ^ Niessen, K. A.; Xu, M.; George, D. K.; Chen, M. C.; Ferre-D-Amare, A. R.; Snell, E. H.; Cody, V.; Pace, J.; Schmidt, M.; Markelz, A. G. (2019). "Protein and RNA dynamical fingerprinting". Nature. 10 (1): 1026. Bibcode:2019NatCo..10.1026N. doi:10.1038/s41467-019-08926-3. PMC 6399446. PMID 30833555. S2CID 70350342.
- ^ Davies, A. Giles; Burnett, Andrew D.; Fan, Wenhui; Linfield, Edmund H.; Cunningham, John E. (2008). "Terahertz spectroscopy of explosives and drugs". Materials Today. 11 (3): 18–26. doi:10.1016/s1369-7021(08)70016-6.
- ^ M.Suzuki and M. Tonouchi (2005). "Fe-implanted InGaAs terahertz emitters for 1.56μm wavelength excitation". Applied Physics Letters. 86 (5): 051104. Bibcode:2005ApPhL..86e1104S. doi:10.1063/1.1861495.
- ^ a b R.J.B. Dietz; B. Globisch; M. Gerhard; et al. (2013). "64 μW pulsed terahertz emission from growth optimized InGaAs/InAlAs heterostructures with separated photoconductive and trapping regions". Applied Physics Letters. 103 (6): 061103. Bibcode:2013ApPhL.103f1103D. doi:10.1063/1.4817797.
- ^ L. Duvillaret; F. Garet; J.-F. Roux; J.-L. Coutaz (2001). "Analytical modeling and optimization of terahertz time-domain spectroscopy experiments, using photoswitches as antennas". IEEE Journal of Selected Topics in Quantum Electronics. 7 (4): 615–623. Bibcode:2001IJSTQ...7..615D. doi:10.1109/2944.974233.
Further reading
- C. A. Schmuttenmaer (2004). "Exploring dynamics in the far-infrared with terahertz spectroscopy" (PDF). Chemical Reviews. 104 (4): 1759–1779. doi:10.1021/cr020685g. PMID 15080711. Archived from the original (PDF) on July 8, 2007.

















