labels = {"f(\[Omega])\[Proportional] \[CapitalPi](\[Omega])", "f(\[Omega])\[Proportional] \[CapitalLambda](\[Omega])", "f(\[Omega])\[Proportional] \!\(\*SuperscriptBox[\(e\), \\(-\*SuperscriptBox[\(\[Omega]\), \(2\)]\)]\)", "f(\[Omega])\[Proportional] \!\(\*SuperscriptBox[\(sech\), \\(2\)]\)(\[Omega])", "f(\[Omega])\[Proportional] \!\(\*SuperscriptBox[\(e\), \(-\(\(|\)\\(\[Omega]\)\(|\)\)\)]\)"};
frames = Table[
Table[
GraphicsRow[{
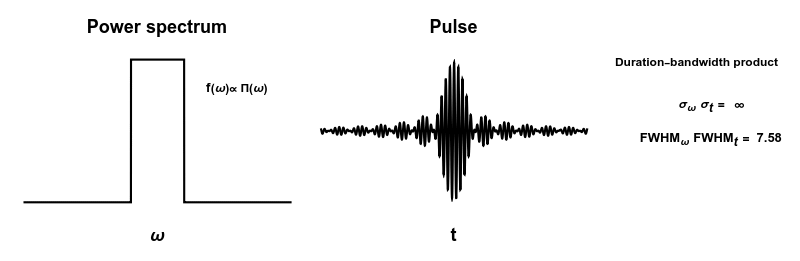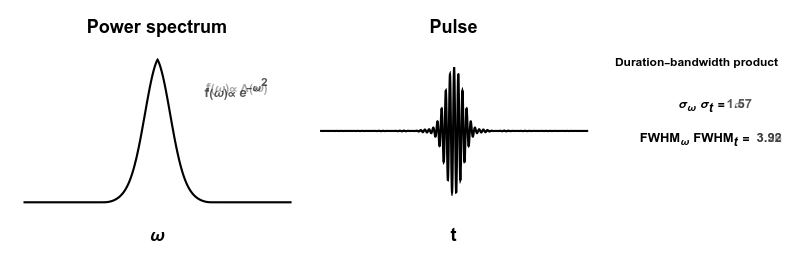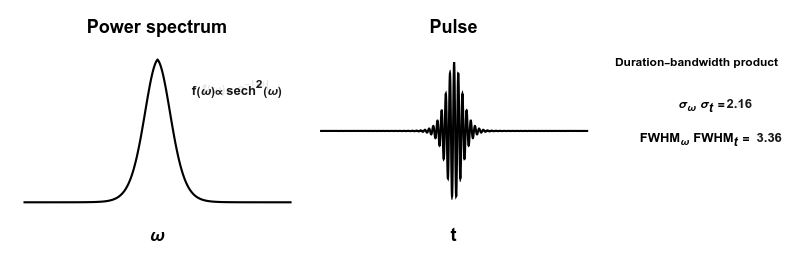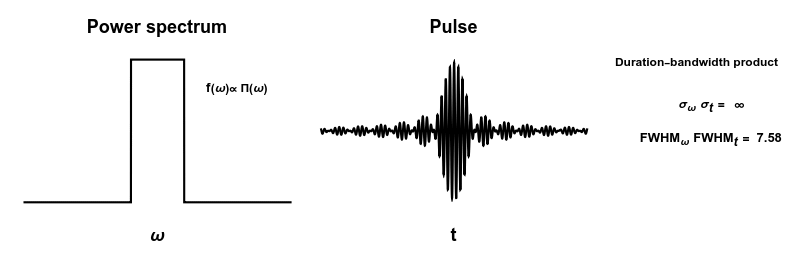
Plot[(1 - \[Tau]) f[[j]]^2 + \[Tau] f[[Mod[j + 1, 5, 1]]]^2, {\[Omega], -5, 5}, PlotRange -> {-0.1, 1.1}, Exclusions -> None, PlotStyle -> Black, Axes -> False, FrameLabel -> {{None, None}, {"\[Omega]", "Power spectrum"}}, Frame -> True, FrameStyle -> Directive[White, FontColor -> Black], LabelStyle -> {FontSize -> 14, Bold}, FrameTicks -> None, Epilog -> {Opacity[1 - \[Tau]], Text[Style[labels[[j]], Black, Bold], {3, 0.8}], Opacity[\[Tau]], Text[Style[labels[[Mod[j + 1, 5, 1]]], Black, Bold], {3, 0.8}]}
]
,
Plot[(1 - \[Tau]) p[[j]]*Cos[\[Omega]0 t] + \[Tau] p[[Mod[j + 1, 5, 1]]]*Cos[\[Omega]0 t], {t, -20, 20}, PlotStyle -> Black, PlotRange -> {-1, 1}, Axes -> False, FrameLabel -> {{None, None}, {"t", "Pulse"}}, Frame -> True, FrameStyle -> Directive[White, FontColor -> Black], LabelStyle -> {FontSize -> 14, Bold}, FrameTicks -> None]
,
Graphics[{Text[Style["Duration-bandwidth product", Black, Bold, FontSize -> 9], {0, 0.8}],
Text[Style["\!\(\*SubscriptBox[\(\[Sigma]\), \(\[Omega]\)]\) \!\(\\*SubscriptBox[\(\[Sigma]\), \(t\)]\) = ", Black, Bold, FontSize -> 10], {0.08, 0.3}], Opacity[1 - \[Tau]],
Text[Style[StringForm["``", NumberForm[\[Sigma]\[Omega][[j]]*\[Sigma]t[[j]] // N, {3, 2}]], Black, Bold, FontSize -> 10], {0.5, 0.32}], Opacity[\[Tau]],
Text[Style[StringForm["``", NumberForm[\[Sigma]\[Omega][[Mod[j + 1, 5, 1]]]*\[Sigma]t[[Mod[j + 1, 5, 1]]] // N, {3, 2}]], Black, Bold, FontSize -> 10], {0.5, 0.32}], Opacity[1],
Text[Style["\!\(\*SubscriptBox[\(FWHM\), \(\[Omega]\)]\) \\!\(\*SubscriptBox[\(FWHM\), \(t\)]\) = ", Black, Bold, FontSize -> 10], {0, -0.1}], Opacity[1 - \[Tau]],
Text[Style[StringForm["``", NumberForm[fwhm\[Omega][[j]]*fwhmt[[j]], {3, 2}]], Black, Bold, FontSize -> 10], {0.85, -0.08}], Opacity[\[Tau]],
Text[Style[StringForm["``", NumberForm[fwhm\[Omega][[Mod[j + 1, 5, 1]]]*fwhmt[[Mod[j + 1, 5, 1]]], {3, 2}]], Black, Bold, FontSize -> 10], {0.85, -0.08}]
}, PlotRange -> {{-1, 1}, {-1, 1}}]
}]
, {\[Tau]1, 0, 1, 0.02}]
, {j, 1, 5}];
ListAnimate[Join[Flatten@Table[{Table[frames[[j, 1]], {10}], frames[[j]]}, {j, 1, 5}] ]]